Confinement et théorie des graphes

Le post d’aujourd’hui porte sur feue la période confinée que nous venons de vivre. Un post toujours graphique bien sûr, mais avec des mathématiques dedans… noooon ne fuyez pas, vous allez voir ça va bien se passer !

Voici la trace GPS obtenue en réalisant l’objectif que je m’étais fixé pendant le confinement, qui était de parcourir à pieds TOUTES les routes et TOUS les chemins à l’intérieur du cercle de 1km de rayon autour de chez moi autorisé pour les sorties dédiées à l’activité physique (*)

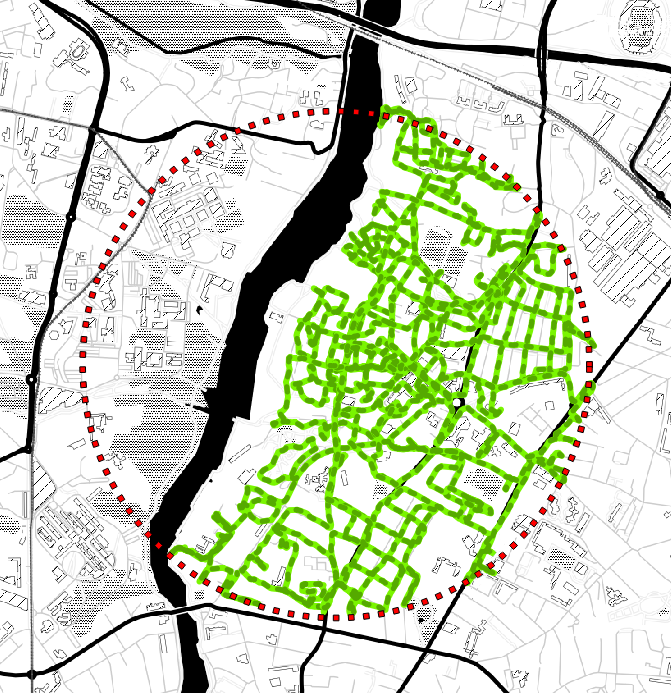
Voyant cette carte, quelqu’un m’a demandé : « Est-il possible de faire ce parcours sans repasser deux fois par la même route ou le même chemin (en enlevant les impasses) ? »
Voilà ce que je lui ai dit :
– pour mon quartier la réponse est clairement non,
– dans le cas général, la réponse est que… ça dépend de la configuration du quartier ! Il y a toutefois une règle simple intéressante à connaître. La voici.

Faisons d’abord les hypothèses suivantes :

• Dans le quartier il y a des routes & des chemins – dans la suite je parlerai seulement de « routes » – branchées sur des « carrefours ».
• Cet ensemble de routes et de carrefours forme un « réseau » (en maths on appelle ça un « graphe »).
• Le réseau est en un seul morceau.
• L’extrémité d’une impasse est un carrefour un peu particulier, avec une seule route branchée dessus.

La règle est la suivante :
Un parcours sans repasser deux fois sur la même route est possible seulement s’il existe zéro ou deux carrefours avec un nombre impair de routes branchées dessus.

Voilà. Simple, non ?
Pas simple pour vous ? Essayez le petit jeu de l’enveloppe.

Dans la plupart des quartiers réels la règle n’est pas respectée : il existe de nombreux carrefours impairs (impasses par exemple), d’où l’impossibilité d’un parcours sans repasser par la même route.

On pourrait raffiner en se demandant si on peut faire le parcours en revenant à son point de départ… Ou en se fixant un point de départ particulier… Toutes ces questions s’étudient mathématiquement en faisant appel à la théorie des graphes, dont la règle ci-dessus (dite « théorème d’Euler« ) fait partie.

Voilà, vous ne pouviez pas continuer à vivre sans savoir cela, n’est-ce pas ?
Vous pouvez maintenant reprendre le cours normal de vos activités.

Philippe

(*) pourquoi un tel objectif me demanderez-vous ? Et je vous répondrai : pourquoi pas ?