C’est quoi une courbe « exponentielle » ?

[Temps de lecture moyen 8 min]

Nous entendons tous en ce moment, dans les médias, parler de l’incidence du coronavirus qui suit une « courbe exponentielle » depuis le mois de juillet. Mais de quoi parle-t’on exactement en disant cela ?
Dans cet article je vais tâcher de vous faire comprendre ce qu’est une exponentielle. Pas de panique hein, si vous êtes un fidèle lecteur vous commencez à me connaître : cet article ne sera pas du tout un cours de maths : je m’engage sur le fait qu’il ne contient aucune formule mathématique et que vous allez tout comprendre !

Dans l’expression « courbe exponentielle » il y a le mot « courbe » et il y a le mot  » exponentielle ».

Qu’est-ce qu’une « courbe » ?

On utilise ce mot pour parler d’un graphique qui comporte :
– un axe horizontal gradué avec une unité représentant une grandeur,
– un axe vertical gradué avec une autre unité représentant une autre grandeur,
– une ligne ( la « courbe ») qui matérialise les valeurs que peut prendre la grandeur de l’axe vertical en fonction de celles de l’axe horizontal.

Pour beaucoup de courbes – c’est notamment le cas pour les courbes qui nous sont présentées pour parler de l’évolution du virus – la grandeur de l’axe horizontal est le temps, gradué en jours, ou semaines, ou mois…
(Dans toute la suite de l’article nous parlerons uniquement des cas où l’axe horizontal est le temps.)
Sur l’axe vertical on peut trouver des grandeurs extrêmement diverses : taux d’incidence du virus, nombre de décès, nombre de personnes en réanimation, etc…

Qu’est ce qu’une « exponentielle » ?

Ce mot désigne une forme particulière que peut prendre la courbe.
Il existe de nombreuses typologies de formes de courbes ; pour ne pas avoir à rentrer dans des notions mathématiques (ouf), on va seulement évoquer deux grandes typologies que l’on va comparer :

1- les courbes linéaires :
elles sont représentées par une ligne droite. Ce type de courbe est obtenu quand une quantité évolue de la façon suivante : à chaque unité de temps, on ajoute une quantité fixe : la ligne monte, toujours eu même rythme, c’est une ligne droite :

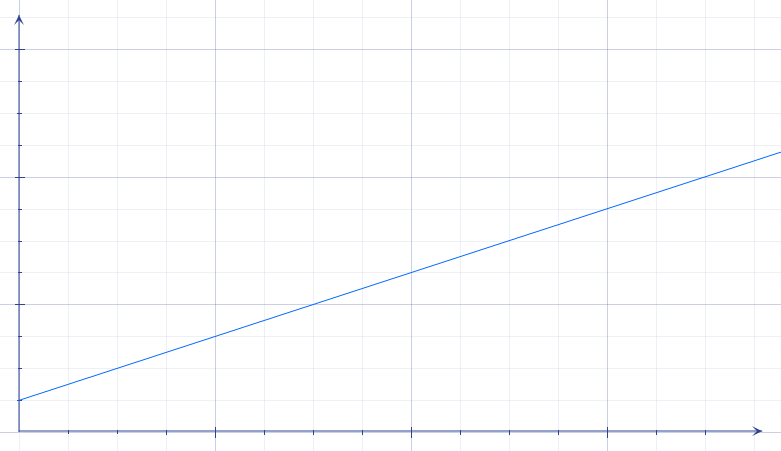
Exemple
Si tous les jours j’achète 12 œufs, la quantité d’œufs que je possède va suivre une évolution linéaire jour après jour : 12, 24, 36, 48, 60… comme sur la courbe ci-dessus.

2- les courbes exponentielles :
elles sont représentées par une ligne concave. Ce type de courbe est obtenu quand, à chaque unité de temps, on multiplie la quantité par un facteur fixe : la ligne monte de plus en plus vite.

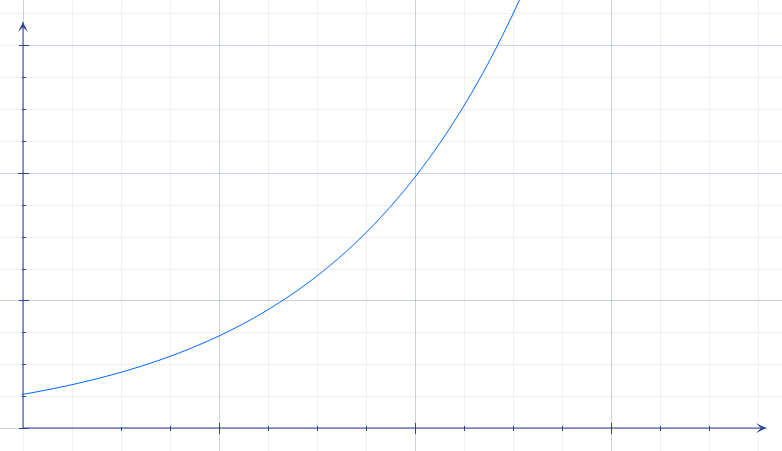
Exemple
Si tous les jours j’achète 2 fois plus d’œufs que la veille, la quantité d’œufs que j’achète va suivre une évolution exponentielle jour après jour : 12, 24, 48, 96, 192… comme sur la courbe ci-dessus.

Une courbe exponentielle est une courbe dont la vitesse de croissance augmente sans arrêt : elle ne cesse d’accélèrer ! En général, les phénomènes représentés par de type de courbe sont des phénomènes explosifs, non maîtrisés, de type réaction en chaine incontrôlée, comme par exemple le nombre de personnes contaminées par un virus dans une population, ou le nombre de descendants d’un couple de lapins qui se reproduisent, puis les petits lapinous se reproduisent à leur tour, etc…

Ces phénomènes sont redoutables car ils peuvent démarrer très progressivement, puis accélérer doucement sans qu’on se rende compte de leur caractère exponentiel, puis nous surprendre lorsque l’accélération devient plus forte.

La mare aux nénuphars
Pour illustrer ce qu’est un phénomène exponentiel et aider à comprendre sa dynamique, la petite devinette suivante est très éclairante.
Imaginez un lac, dans lequel il y a des nénuphars. Ceux-ci se multiplient de sorte que chaque jour, chaque feuille de nénuphar produit une autre feuille de nénuphar. Au bout de trente jours, la totalité du lac est couverte et l’espèce meurt étouffée, privée d’espace et de nourriture. Au bout de combien de jours les nénuphars ont-ils couvert la moitié du lac ?
[prenez 20 secondes pour réfléchir avant de lire la suite…]
Notre cerveau a tendance a répondre instinctivement en suivant une règle de proportionnalité : la moitié du lac, donc la moitié de 30 jours, donc 15 jours. Or c’est faux, la réponse est 29 jours ! En effet, étant donné que le surface des nénuphars double chaque jour, si le 29è jour la moitié du lac est remplie, alors le lendemain c’est tout le lac qui sera rempli.

Le cerveau humain n’est pas fait pour bien appréhender ces phénomènes : naturellement, notre cerveau raisonne de façon proportionnelle et il est adapté aux phénomènes linéaires (représentés par les courbes linéaires cf ci-dessus). Il pense instinctivement que la variation d’une cause va engendrer une variation proportionnelle de la conséquence, or ce n’est pas ce qui se produit lorsqu’un phénomène évolue exponentiellement : la conséquence d’une variation de la cause est beaucoup plus importante que ce à quoi l’on s’attend instinctivement. Nous sommes donc, nous, humains, très mal armés pour ressentir, comprendre et anticiper le comportement des phénomènes exponentiels.
C’est certainement la raison pour laquelle nous avons pu entendre ces jours-ci dans la bouche de nos responsables nationaux, que l’évolution récente du virus a « surpris » tout le monde. En fait non, elle n’est hélas pas surprenante et les spécialistes ne l’ont pas été (surpris), c’est juste que l’évolution du virus est exponentielle (tant qu’un facteur externe ne permet pas de la juguler : vaccin, mesures de confinement, barrières sanitaires,…) et elle prend donc notre cerveau au dépourvu…

Je vais vous donner un exemple de courbe que l’on ne pense pas être exponentielle… et pourtant c’est le cas.
Le voici : lorsqu’une quantité augmente de x% par unité de temps, c’est une variation exponentielle ! Même si x n’est pas grand, par exemple quelques pourcents, inéluctablement la quantité va augmenter de plus en plus vite jusqu’à atteindre des valeurs et une vitesse de croissance très importante.

Illustrons cela par le cas de la croissance économique d’un pays : partout dans le monde, elle est exprimée en pourcentage annuel d’augmentation du PIB. Prenons l’hypothèse d’une croissance de 2% par an (hypothèse optimiste, par les temps qui courent) et traçons la courbe de l’évolution du PIB de la France dans les prochaines décennies :

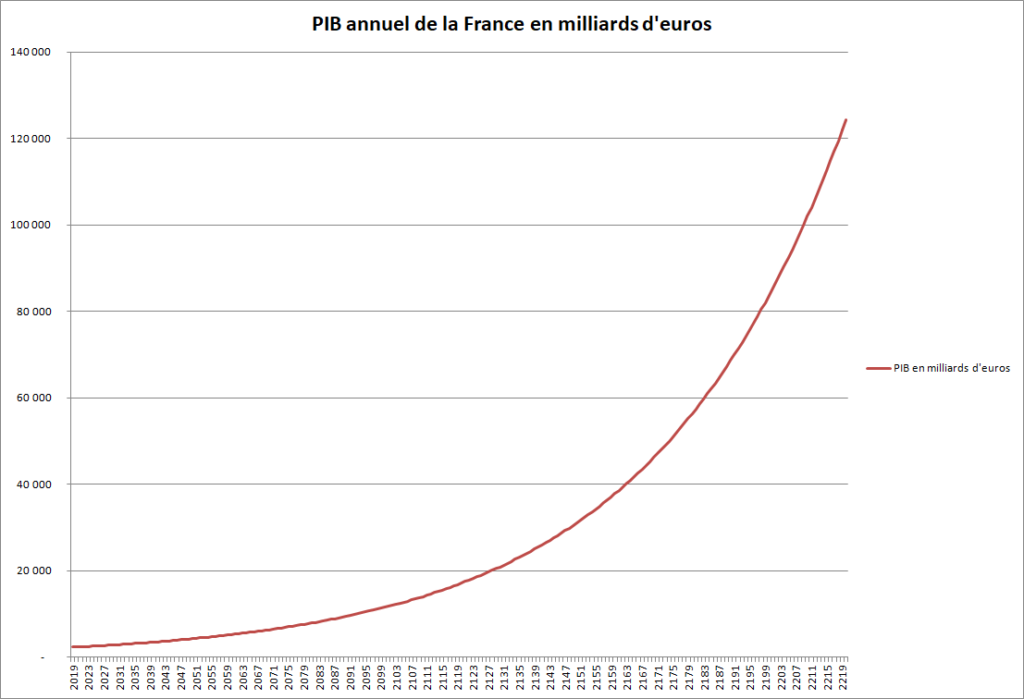
Le PIB annuel actuel (2019) de la France est de 2 322 milliards d’euros. En 2120, au rythme de 2% par an il serait de plus de 17 000 milliards d’euros annuels… et en 2220 de 124 000 milliards d’euros !! Soit une multiplication par… 7 en 100 ans, et par plus de 50 en 200 ans (vérifiez, faites le calcul). Énooorme, non ?

Nota Pour ceux qui doutent sur le caractère exponentiel d’une augmentation régulière de 2%, songez que cela revient à multiplier chaque année le PIB de l’année précédente par 1,02. C’est bien la définition d’une exponentielle comme indiqué ci-dessus : on multiplie à chaque unité de temps par un facteur fixe (supérieur à 1 bien sûr).

Appliquez cela par exemple au marché de l’automobile : il y a aujourd’hui environ 1,5 milliards de voiture sur Terre, si la croissance économique est de 2% pendant encore 100 ans et si on fait l’hypothèse que le marché de l’automobile croîtra au même rythme, alors dans un siècle il y aura 10,5 milliards de voitures sur Terre, puis si ça continue encore 100 ans nous aurons 78 milliards de voiture dans 200 ans, soit plusieurs voitures pour chaque personne sur Terre y compris les enfants ! Vous allez me rétorquer que j’exagère, que le taux de croissance pour le marché de l’automobile est plutôt celui du chiffre d’affaire des constructeurs et non celui du nombre d’automobiles, OK. Ceci étant, le principe reste : une croissance économique basée sur une augmentation annuelle de x% du PIB est une croissance exponentielle, c’est mathématique.

Épilogue

En mathématiques, une exponentielle ne s’arrête jamais et continue de plus en plus rapidement jusqu’à l’infini. Dans le monde réel, c’est bien sûr impossible. Au bout d’un moment, il survient toujours un phénomène externe qui fait que l’évolution s’arrête ou se stabilise, il ne peut en être autrement :
– la propagation d’un virus finit par être limitée par la population des individus à contaminer,
– les lapins qui se reproduisent sans cesse finissent par être limités pas l’espace et la quantité de nourriture à leur disposition.
Dans la vraie vie, l’infini n’existe pas ! (*)

Pour aller plus loin
Rapprochons le constat du caractère exponentiel de la croissance économique du fait que :
– la Terre et ses ressources minières et énergétiques non renouvelables sont parfaitement finies et limitées (la Terre ne fait que 6300 km de rayon),
– ces ressources sont, respectivement, les matières premières et les carburants de la croissance économique,
et réfléchissons deux secondes à la conclusion que l’on peut en tirer.
Il viendra nécessairement un jour où les ressources ne seront pas suffisantes pour soutenir une croissance économique exponentielle. Qu’on le veuille ou non, une croissance économique perpétuelle à x% par an est une impasse, à cause du manque de ressources qui, elles, sont fixées une fois pour toutes. La seule question qui subsiste est quand ? Quand atteindrons nous les limites physiques liées à la finitude des ressources non renouvelables de la Terre ? Cette question est redoutablement complexe, et pour chacune des ressources que nous utilisons (pétrole, charbon, gaz, aluminium, platine, argent, lithium, cobalt, cuivre, etc…), il serait possible d’écrire des livres entiers pour en débattre.
Dans un prochain article je me risquerai à l’exercice pour l’une de ces ressources, une des plus importantes : le pétrole.

Quelques liens

• Pour ceux qui ne sont pas allergiques aux formules mathématiques :
  https://fr.wikipedia.org/wiki/Croissance_exponentielle

• Pour ceux qui sont un peu allergiques aux formules mathématiques mais pas trop (tolérance aux faibles doses) :
  https://fr.vikidia.org/wiki/Fonction_exponentielle

• Pour tous, allergiques et non allergiques, des expériences pour mieux appréhender la croissance exponentielle :
  https://pixees.fr/des-experiences-pour-mieux-apprehender-la-croissance-exponentielle/ (euh après relecture, il y a quand même quelques formules qui traînent… ;-) )

(*) « Dans la vraie vie, l’infini n’existe pas. »
Mmmh, est-ce bien sûr ? Qu’en pensez-vous ? Vous avez deux heures !